Why the SAT Book's Explanations Are Absurd

The Math section of the SAT now tests higher-level concepts that students can expect to encounter in Algebra II (and in some cases, even Precalculus). This means that SAT Math is already difficult enough: as juniors, many students are only in the middle of Algebra II, and haven’t yet learned or fully comprehended some topics that appear on the SAT. Having the general interest of students in mind, and promoting its self-professed goal of leveling the playing field in test prep, the College Board offers SAT Practice Test answer explanations that are crystal clear and written in a way that will help the average student improve his or her test performance, right?
Wrong. Very wrong.
Case in point? The October 2016 SAT has just been released, and a single question from the Math’s No Calculator section demonstrates my point perfectly. Here’s the question.
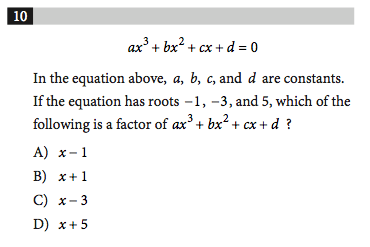
And here's the explanation.

Yeah, okay. I thought this was supposed to be an answer “explanation”, not an answer “obfuscation”.
Nothing here is technically wrong, but there are at least three major issues with this answer.
- To any student outside of those who qualify to attend the International Mathematical Olympiad, this is pure gibberish. It’s an explanation written for mathematicians, full stop. Give this to average students, and even if their eyes don’t glaze over, they will be so intimidated and perplexed by the language that they will leave the explanation certain they’ll never be able to get a question like this correct.
- No sane person––even math nerds like yours truly––would (or should) actually solve the problem by thinking this way. That’s right: it’s a genuinely bad approach that doesn't allow an application of a broader strategy.
- The answer is explained assuming knowledge of the correct answer. Notice how the second sentence begins by assuming that we’re dividing the polynomial by x + 1, which is the right choice. Well, if we know enough to assume that, then we probably don’t need the explanation in the first place.
The real way to solve this problem is demonstrated in the video below. It connects polynomial functions and their graphs in a very simple way––students will understand it, and more importantly, will be able to use it again when they encounter a similar problem. That's the whole point of practice, isn't it?
This is only the tip of the Method Test Prep iceberg. If you want to see how our program––which features hundreds of videos just like the one above––can help you avoid the College Board's "explanations" and make true progress, check out our program here.


